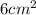Answer:
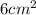
Explanation:
Let x and y be the sides of the rectangle.
Area of the Triangle, A(x,y)=xy
From the diagram, Triangle ABC is similar to Triangle AKL
AK=4-y
Therefore:
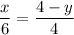
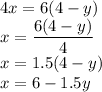
We substitute x into A(x,y)
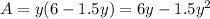
We are required to find the maximum area. This is done by finding
the derivative of Aand solving for the critical points.
Derivative of A:
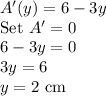
Recall that: x=6-1.5y
x=6-1.5(2)
x=6-3
x=3cm
Therefore, the maximum rectangle area is:
Area =3 X 2 =