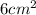Question

Find the area of the largest rectangle that can be inscribed in a right triangle with legs of lengths 4 cm and 6 cm if two sides of the rectangle lie along the legs. webassign cengage

Answer 1

`6cm^2`

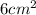
Explanation:

Let x and y be the sides of the rectangle.

Area of the Triangle, A(x,y)=xy

From the diagram, Triangle ABC is similar to Triangle AKL

AK=4-y

Therefore:

`(x)/(6) =(4-y)/(4)`

`4x=6(4-y)\\x=(6(4-y))/(4) \\x=1.5(4-y)\\x=6-1.5y`

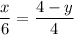
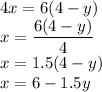
We substitute x into A(x,y)

`A=y(6-1.5y)=6y-1.5y^2`

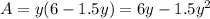
We are required to find the maximum area. This is done by finding

the derivative of Aand solving for the critical points.

Derivative of A:

`A'(y)=6-3y\\$Set $A'=0\\6-3y=0\\3y=6\\y=2$ cm`

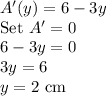
Recall that: x=6-1.5y

x=6-1.5(2)

x=6-3

x=3cm

Therefore, the maximum rectangle area is:

Area =3 X 2 =
`6cm^2`