Answer:
7.4inches
Explanation:
Check the attachment for the diagram. Sine rule will be used to get the unknown side of the triangle.
According to the rule;
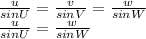
Given w = 3 in, ∠W=23° and ∠U=73°, on substituting into the equation above to get u we have;

The length of u is 7.4inches to nearest 10th of an inch