Question

Given below are seven observations collected in a regression study on two variables, x (independent variable) and y (dependent variable). Develop the least squares estimated regression equation. What is the coefficient of determination? x y 2 12 3 9 6 8 7 7 8 6 7 5 9 2

Answer 1

Explanation:

Hello!

Given the independent variable X and the dependent variable Y (see data in attachment)

The regression equation is

^Y= b₀ + bX

Where

b₀= estimation of the y-intercept

b= estimation of the slope

The formulas to manually calculate both estimations are:

`b= (sumXY-((sumX)(sumY))/(n) )/(sumX^2-((sumX)^2)/(n) )`

`b_0= \frac{}{y} - b*\frac{}{x}`

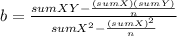
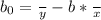
n=7

∑X= 42

∑X²= 292

∑Y= 49

∑Y²= 403

∑XY= 249

`\frac{}{y} = (sumY)/(n) = (49)/(7) = 7`

`\frac{}{x} = (sumX)/(n) = (42)/(7) = 6`

`b= (249-(42*49)/(7) )/(292-(42^2)/(7) )= -1.13`

`b_0= 7- (-1.13)*6= 13.75`

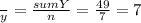
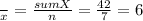
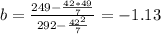
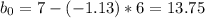
^Y= 13.75 - 1.13X

Using the raw data you can calculate the coefficient of determination as:

`R^2= (b^2[sumX^2-((sumX)^2)/(n) ])/([sumY^2-((sumY)^2)/(n) ])`

`R^2= ((-1.13)^2[292-((42)^2)/(7) ])/([403-((49)^2)/(7) ])= 0.84`

This means that 84% of the variability of the dependent variable Y is explained by the response variable X under the model ^Y= 13.75 - 1.13X

I hope this helps!