Answer:
the range of K can be said to be : -3.59 < K< 0.35
Step-by-step explanation:
The transfer function of a typical tape-drive system is given by;
![KG(s) = (K(s+4))/(s[s+0.5)(s+1)(s^2+0.4s+4)])](https://img.qammunity.org/2021/formulas/engineering/college/uwa0jld73t72bjzxavr1v2qeijm4vbzugb.png)
calculating the characteristics equation; we have:
1 + KG(s) = 0
![1+ (K(s+4))/(s[s+0.5)(s+1)(s^2+0.4s+4)]) = 0](https://img.qammunity.org/2021/formulas/engineering/college/2shkg1g8h4ngsyqtrpu5x3tu47wz9wjgz6.png)
![{s[s+0.5)(s+1)(s^2+0.4s+4)]} +{K(s+4)}= 0](https://img.qammunity.org/2021/formulas/engineering/college/7tmczqtpdhak40fq3ed0er0d3cdu3mmdyu.png)
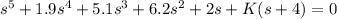
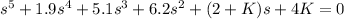
We can compute a Simulation Table for the Routh–Hurwitz stability criterion Table as follows:
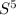 1 5.1 2+ K
1 5.1 2+ K
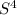 1.9 6.2 4K
1.9 6.2 4K
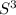 1.83
1.83
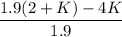 0
0
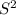
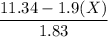 4K 0
4K 0
S
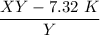 0 0
0 0
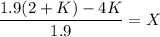
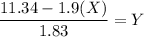
We need to understand that in a given stable system; all the elements in the first column is usually greater than zero
So;
11.34 - 1.9(X) > 0
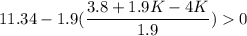
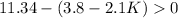
7.54 +2.1 K > 0
2.1 K > - 7.54
K > - 7.54/2.1
K > - 3.59
Also
4K >0
K > 0/4
K > 0
Similarly;
XY - 7.32 K > 0
![((3.8+1.9K-4K)/(1.9))[11.34 - 1.9((3.8+1.9K-4K)/(1.83)) > 7.32 \ K]](https://img.qammunity.org/2021/formulas/engineering/college/gmg4nld12dxhvtbmln0ndhze4h4al7vk86.png)
0.54(2.1K+7.54)>7.32 K
11.45 K < 4.07
K < 4.07/11.45
K < 0.35
Thus the range of K can be said to be : -3.59 < K< 0.35