Question

Triangles O N M and S R Q are shown. Angles O N M and S R Q are congruent. The length of side N M is 10 and the length of side S R is 20. The length of side N O is 8 and the length of side Q R is x. What value of x will make △ONM similar to △SRQ by the SAS similarity theorem? 16 20 25 50

Answer 1

Answer:(C) 25

Explanation:

took the test

Answer 2

Option C.

Explanation:

In △ONM and △SRQ,

`\angle ONM\cong \angle SRQ`

`NM=10`

`SR=20`

`NO=8`

`QR=x`

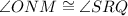
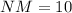
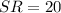
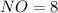
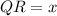
We need to find the value of x that will make △ONM similar to △SRQ by the SAS similarity theorem.

According to SAS similarity theorem, two triangle are similar if two corresponding sides in both triangles are proportional and the included angle in both are congruent.

It is given that
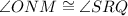`\angle ONM\cong \angle SRQ`. So, both triangles are similar by SAS if

`(NO)/(NM)=(SR)/(QR)`

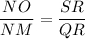
Substitute the given values.

`(8)/(10)=(20)/(x)`

`8* x=20* 10`

`8x=200`

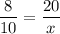
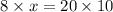
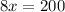
Divide both sides by 8.

`x=(200)/(8)`

`x=25`

Therefore, the correct option is C.