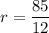Question

LK is tangent to circle J at point K. Circle J is shown. Line segment J K is a radius. Line segment K L is a tangent that intersects at point K. A line is drawn from point L through a point on the circle to the center point J. The length of the radius is r, the length of K L is 11, and the length of the line segment from point L to the point on the circle is 6. What is the length of the radius? StartFraction 6 Over 85 EndFraction StartFraction 85 Over 12 EndFraction StartFraction 121 Over 36 EndFraction StartFraction 157 Over 12 EndFraction

Answer 1

The answer is B on Edge 2020

Explanation:

I did the assignment

Answer 2

`(B)r=(85)/(12)`

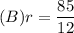
Explanation:

Given a circle centre J

Let the radius of the circle =r

LK is tangent to circle J at point K

From the diagram attached

• LX=6
• Radius, XJ=JK=r
• LK=11

Theorem: The angle between a tangent and a radius is 90 degrees.

By the theorem above, Triangle JLK forms a right triangle with LJ as the hypotenuse.

Using Pythagoras Theorem:

`(6+r)^2=r^2+11^2\\(6+r)(6+r)=r^2+121\\36+6r+6r+r^2=r^2+121\\12r=121-36\\12r=85\\r=(85)/(12)`

The length of the radius,
`r=(85)/(12)`