Answer:
1).
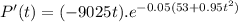
2). (-435.36) dollars per week
Explanation:
Weekly price decay of the product is represented by the function,
P(x) =
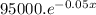
And the price of the product changes over the period of 't' weeks is represented by,
x(t) =

Function representing the rate of change in the profit with respect to the time will be represented by,
1). P'(t) =
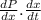
Since, P(x) =
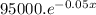
P'(x) =
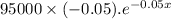
=
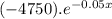
Since, x(t) = 53 + 0.95t²
x'(t) = 1.9t

By substituting x = 53 + 0.95t²
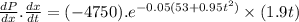
P'(t) =
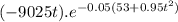
2). For t = 7 weeks,
P'(7) =
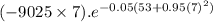
=
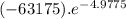
= (-63175)(0.006891)
= (-435.356) dollars per week
≈ (-435.36) dollars per week