Answer:
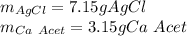
Step-by-step explanation:
Hello,
In this case, with the given information, we can identify the limiting reactant and compute the theoretical yield for the undergoing chemical reaction:
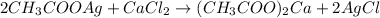
Thus, with the given concentrations and volumes we compute the available moles of silver acetate:
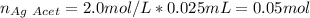
Then, the moles of silver acetate that are consumed by 35 mL of 1.0 M calcium chloride:
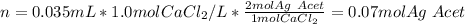
Therefore, since there are less available moles, it is the limiting reactant, for that reason, the theoretical yields of both calcium acetate and silver acetate are:
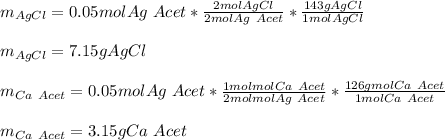
Best regards.