Question

25 ml of 2.0 M silver acetate reacts with grams 35 ml of 1.0 M Calcium chloride

Answer 1

`m_(AgCl)=7.15gAgCl\\m_(Ca\ Acet)=3.15gCa\ Acet\\`

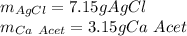
Step-by-step explanation:

Hello,

In this case, with the given information, we can identify the limiting reactant and compute the theoretical yield for the undergoing chemical reaction:

`2CH_3COOAg+CaCl_2\rightarrow (CH_3COO)_2Ca+2AgCl`

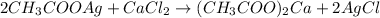
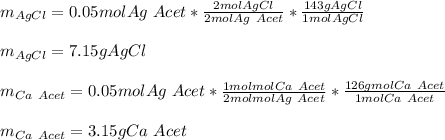
Thus, with the given concentrations and volumes we compute the available moles of silver acetate:

`n_(Ag\ Acet)=2.0mol/L*0.025mL=0.05mol`

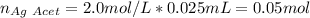
Then, the moles of silver acetate that are consumed by 35 mL of 1.0 M calcium chloride:

`n=0.035mL*1.0molCaCl_2/L*(2mol Ag\ Acet)/(1molCaCl_2) =0.07mol Ag\ Acet`

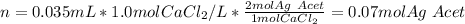
Therefore, since there are less available moles, it is the limiting reactant, for that reason, the theoretical yields of both calcium acetate and silver acetate are:

`m_(AgCl)=0.05mol Ag\ Acet*(2molAgCl)/(2mol Ag\ Acet) *(143gAgCl)/(1molAgCl) \\\\m_(AgCl)=7.15gAgCl\\\\m_(Ca\ Acet)=0.05mol Ag\ Acet*(1molmol Ca\ Acet)/(2molmol Ag\ Acet) *(126gmol Ca\ Acet)/(1mol Ca\ Acet) \\\\m_(Ca\ Acet)=3.15gCa\ Acet`

Best regards.