Question

Q2(i). A line “t” is parallel to 3y = 6x + 9. Find the slope of this line “t”. (ii) Another line “r” is perpendicular to the line 3y = 6x + 9. Find the gradient of the line “r”.

Answer 1

(i) The slope of line 'T' is 2.

(ii) The slope of line 'R' is -
`(1)/(2)`

Explanation:

(i) A line 'T' is parallel to line whose equation is; 3y = 6x + 9

We are to find the slope of this line;

The slopes of two parallel lines is the same.

To put the equation of our second line in cartesian plane format;

3y = 6x + 9

Dividing throughout by 3 we get;

y = 2x + 3

So the slope of our line is 2 and so the slope of the line 'T' is 2.

(ii) Another line 'R' is perpendicular to the line whose equation is 3y = 6x + 9

We are to find the gradient/slope of this line;

The product of any two perpendicular lines is -1.

To put the equation of our second line in cartesian plane format;

3y = 6x + 9

Dividing throughout by 3 we get;

y = 2x + 3

The slope of our second line is 2

Let the slope of line 'R' equal to a

So a × 2 = -1

Hence the slope of our line 'R' = a =
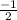`(-1)/(2)` = -
`(1)/(2)`