Question

For better thermal control it is common to make catalytic reactors that have many tubes packed with catalysts inside a larger shell (just like a shell and tube heat exchanger). Consider one tube inside such a reactor that is 2.5 m long with an inside diameter of 0.025 m. The catalyst is alumina spheres with a diameter of 0.003 m. The particle density is 1300 kg/m3 and the bed void fraction is 0.38. Compute the pressure drop seen for a superficial mass flux of 4684 kg/m2hr. The feed is methane at a pressure of 5 bar and 400 K. At these conditions the density of the gas is 0.15 mol/dm-3 and the viscosity is 1.429 x 10-5 Pa s.

Answer 1

the pressure drop is 0.21159 atm

Step-by-step explanation:

Given that:

length of the reactor L = 2.5 m

inside diameter of the reactor d= 0.025 m

diameter of alumina sphere
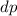`dp`= 0.003 m

particle density = 1300 kg/m³

the bed void fraction
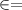`\in =` 0.38

superficial mass flux m = 4684 kg/m²hr

The Feed is methane with pressure P = 5 bar and temperature T = 400 K

Density of the methane gas
`\rho` = 0.15 mol/dm ⁻³

viscosity of methane gas
`\mu` = 1.429 x 10⁻⁵ Pas

The objective is to determine the pressure drop.

Let first convert the Density of the methane gas from 0.15 mol/dm ⁻³ to kg/m³

SO; we have :

Density = 0.15 mol/dm ⁻³

Molar mass of methane gas (CH₄) = (12 + (1×4) ) = 16 mol

Density =
`0.1 5 *(16)/(0.1^3)`

Density = 2400

Density
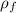`\rho_f` = 2.4 kg/m³

Density = mass /volume

Thus;

Volume = mass/density

Volume of the methane gas = 4684 kg/m²hr / 2.4 kg/m³

Volume of the methane gas = 1951.666 m/hr

To m/sec; we have :

Volume of the methane gas = 1951.666 * 1/3600 m/sec = 0.542130 m/sec

`Re = (dV \rho)/(\mu)`

`Re = (0.025*0.5421430*2.4)/(1.429*10^5)`

`Re=2276.317705`

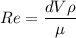
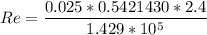
For Re > 1000

`(\Delta P)/(L)=(1.75 \rho_f(1- \in)v_o)/(\phi_sdp \in^3)`

`(\Delta P)/(2.5)=((1.75 *2.4)(1- 0.38)*0.542130)/(1*0.003 (0.38)^3)`

`\Delta P=8575.755212*2.5`

`\Delta = 21439.38803 \ Pa`

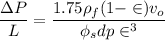
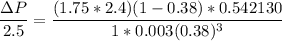
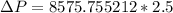
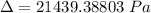
To atm ; we have

`\Delta P = (21439.38803 )/(101325)`

`\Delta P =0.2115903087 \ atm`

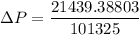
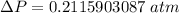
ΔP ≅ 0.21159 atm

Thus; the pressure drop is 0.21159 atm