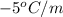Answer:
a)
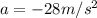
b)
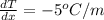
Step-by-step explanation:
a)
In order to solve this problem, we need to start by remembering how the acceleration is related to the velocity of a particle. We have the following relation:
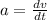
in other words, the acceleration is defined to be the derivative of the velocity function with respect to time. So let's take our speed function:
u=20-2x
if we take its derivative we get:
du=-2dx
this is the same as writting:
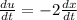
we also know that velocity is defined to be:
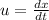
so we get that:
a=-2u
when substituting we get that:
a=-2(20-2x)
when expanding we get:
a=-40+4x
and now we can use this equation to find our acceleration at x=3, so:
a=-40+4(3)
a=-40+12

b)
the same applies to this problem with the difference that this will be the rate of change of the temperature per m. So we proceed and take the derivative of the temperature function:
T=200-5x
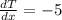
so the rate of change is