Question

What is the range of the function?

The function f(x) = (x - 4)(x - 2) is shown.

10

O all real numbers less than or equal to 3

O all real numbers less than or equal to - 1

O all real numbers greater than or equal to 3

O all real numbers greater than or equal to - 1

Answer 1

The range of the function is all real numbers greater than or equal to -1.

Explanation:

Second order polynomials are continous and have an absolute maximum or minimum that restricts the set of the range associated with the function. A fair approach to estimate the range is rewritting the expression into parabola form, which is:

`y - k = C \cdot (x-h)^(2)`

Where:

`C` - Vertix parameter, dimensionless. If
`C > 0`, then vertix is an absolute minimum, but if
`C < 0`, vertix is an absolute maximum.

`x` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

`h` - Location of the vertix with respect to the independent variable, dimensionless.

`k` - Location of the vertix with respect to the dependent variable, dimensionless. This value restrics the set corresponding to the range of the polynomic function.

First, we have to expand polynomial into its standard form:

`y = (x-4)\cdot (x-2)`

`y = x^(2)-6\cdot x +8`

Now, we are going to complete the square and factorize the resultant expression until parabola form is obtained:

`y = x^(2)-6\cdot x + 9 -9 + 8`

`y = (x-3)^(2) -1`

`y + 1 = 1 \cdot (x-3)^(2)`

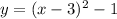
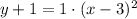
Since the vertix parameter is positive, then vertix is an absolute minimum. The location of the vertix with respect ot the depedent variable is
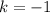`k = -1`. Therefore, the range of the function is all real numbers greater than or equal to -1.