Answer:
The probability that on a randomly selected day the statistics professor will have five messages is 0.1755.
Explanation:
Let the random variable X represent the number of e-mail messages per day a statistics professor receives from students.
The random variable is approximated by the Poisson Distribution with parameter λ = 5.
The probability mass function of X is as follows:
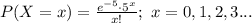
Compute the probability that on a randomly selected day she will have five messages as follows:
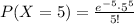

Thus, the probability that on a randomly selected day the statistics professor will have five messages is 0.1755.