Answer:
44.93% probability that the person will need to wait at least 7 minutes total
Explanation:
To solve this question, we need to understand the exponential distribution and conditional probability.
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
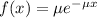
In which
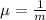 is the decay parameter.
is the decay parameter.
The probability that x is lower or equal to a is given by:
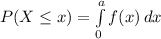
Which has the following solution:
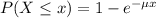
The probability of finding a value higher than x is:
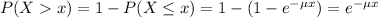
Conditional probability:
We use the conditional probability formula to solve this question. It is
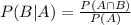
In which
P(B|A) is the probability of event B happening, given that A happened.
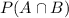 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
The length of time for one individual to be served at a cafeteria is an exponential random variable with mean of 5 minutes
This means that
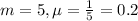
Assume a person has waited for at least 3 minutes to be served. What is the probability that the person will need to wait at least 7 minutes total
Event A: Waits at least 3 minutes.
Event B: Waits at least 7 minutes.
Probability of waiting at least 3 minutes:
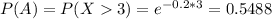
Intersection:
The intersection between waiting at least 3 minutes and at least 7 minutes is waiting at least 7 minutes. So
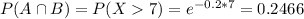
What is the probability that the person will need to wait at least 7 minutes total
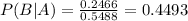
44.93% probability that the person will need to wait at least 7 minutes total