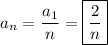2 Answers

Plasmacel · Answer 1 · 2021-03-02T16:24:36+0000

Multiply 2 by 1/2 to get 1.

Multiply 1 by 2/3 to get 2/3.

Multiply 2/3 by 3/4 to get 6/12 = 1/2.

Multiply 1/2 by 4/5 to get 4/10 = 2/5.

Multiply 2/5 by 5/6 to get 10/30 = 1/3.

Multiply 1/3 by 6/7 to get 6/21 = 2/7. (I suspect there's a typo in the question.)

And so on, so that the nth term in the sequence is multiplied by n/(n + 1) to get the (n + 1)th term.

Recursively, the sequence is given by

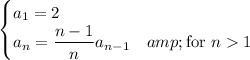
$\begin{cases}a_1=2\\a_n=\frac{n-1}na_(n-1)&\text{for }n>1\end{cases}$

We can solve this exactly by iterating:

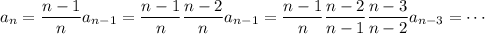
$a_n=\frac{n-1}na_(n-1)=\frac{n-1}n\frac{n-2}na_(n-1)=\frac{n-1}n(n-2)/(n-1)(n-3)/(n-2)a_(n-3)=\cdots$

and so on down to

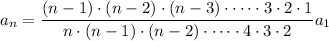
$a_n=((n-1)\cdot(n-2)\cdot(n-3)\cdot\cdots\cdot3\cdot2\cdot1)/(n\cdot(n-1)\cdot(n-2)\cdot\cdots\cdot4\cdot3\cdot2)a_1$

or

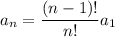
a_n=((n-1)!)/(n!)a_1

and with lots of cancellation, we end up with

$a_n=\frac{a_1}n=\boxed{\frac2n}$

Please log in or register to add a comment.