Answer:
The 99% confidence interval for the percentage of Phoenix residents who support mandatory sick leave for food handlers is between 85.40% and 92.60%.
Explanation:
Confidence interval for the proportion:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
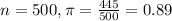
99% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
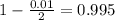 , so
, so
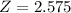 .
.
The lower limit of this interval is:

The upper limit of this interval is:
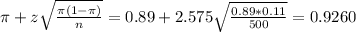
For the percentage:
Multiply the proportion by 100.
0.8540*100 = 85.40%
0.9260*100 = 92.60%
The 99% confidence interval for the percentage of Phoenix residents who support mandatory sick leave for food handlers is between 85.40% and 92.60%.