Answer:
The probability that a randomly selected member of this class of homeowners will not file a claim of either type is 0.89.
Explanation:
Denote the events as follows:
X = liability claim will be filled
Y = property claim will be filled
The information provided is:
P (X) = 0.04
P (Y) = 0.10
P (X ∩ Y') = 0.01
The probability that a randomly selected member of the class of homeowners will not file a claim of either type will be given by:
![P[(X\cup Y)']=1-P(X\cup Y)=1-[P(X)+P(Y)-P(X\cap Y)]](https://img.qammunity.org/2021/formulas/mathematics/college/hpukqp9f5pyklbj3q3salsc622x96rcjvy.png)
According to the law of total probability:
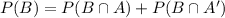
Use the law of total probability to determine the value of P (X ∩ Y) as follows:
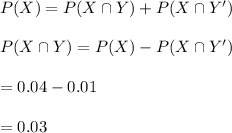
The value of P (X ∩ Y) is 0.03.
Compute the value of P (X ∪ Y) as follows:
![P[(X\cup Y)']=1-P(X\cup Y)](https://img.qammunity.org/2021/formulas/mathematics/college/95d5l6ibjau0b71pmrbyv3bomgn01ly5m6.png)
![=1-[P(X)+P(Y)-P(X\cap Y)]\\\\=1-[0.04+0.10-0.03]\\\\=1-0.11\\\\=0.89](https://img.qammunity.org/2021/formulas/mathematics/college/fq8rjrvis32slpthk67x9bis9avv4fr72v.png)
Thus, the probability that a randomly selected member of this class of homeowners will not file a claim of either type is 0.89.