Question

Which statement justifies that ∠K ≅ ∠N? answers: A) ΔHKL ≅ ΔHMN by ASA; but the two angles aren't congruent because they aren't corresponding angles. B) The two angles aren't congruent. C) ΔHKL ≅ ΔHMN by ASA; ∠K ≅ ∠N because they're corresponding angles in congruent triangles. D) ΔHLK ≅ ΔHMN by AAS; ∠K ≅ ∠N because they're corresponding angles in congruent triangles.

Answer 1

ΔHLK ≅ ΔHMN by AAS; ∠K ≅ ∠N because they're corresponding angles in congruent triangles.

Step-by-step explanation: I took the test

Answer 2

Correct answer is:

D) ΔHLK ≅ ΔHMN by AAS; ∠K ≅ ∠N because they're corresponding angles in congruent triangles.

Explanation:

We are given the diagram, in which there are 2 triangles namely
`\triangle HLK, \triangle HMN`.

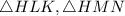1. Side KH = Side NH

2.
`\angle L \cong \angle M`

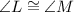
From the given figure, we can derive that:

`\angle KHL \cong \angle NHM`

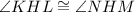
Property used: Vertically opposite angels made by two lines crossing each other are equal.

So, we have two angles (
`\angle L \cong \angle M` and
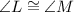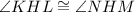`\angle KHL \cong \angle NHM`)of the triangle as same and one side equal from the two given triangles
`\triangle HLK, \triangle HMN`.

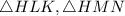So, we can say that the two triangles are congruent.

`\triangle HLK \cong \triangle HMN`

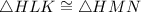
The side is not between the two equal angles, so it is AAS congruence.

And Congruent triangles have their corresponding angles equal.

Therefore, option D) is true :

ΔHLK ≅ ΔHMN by AAS; ∠K ≅ ∠N, because they're corresponding angles in congruent triangles.