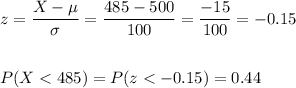Question

The math SAT is scaled so that the mean score is 500 and the standard deviation is 100. Assuming scores are normally distributed, find the probability that a randomly selected student scores

Answer 1

a. P(X>695)=0.026

b. P(X<485)=0.44

Explanation:

The question is incomplete:

a. higher than 695 on the test.

b. at most 485 on the test.

We have a normal distribution with mean 500 and standard deviation of 100 for the test scores. We will use the z-scores to calculate the probabilties with the standard normal distribution table.

a. We want to calculate the probability that a randomly selected student scores higher than 695.

We calculate the z-score and then we calculate the probability:

`z=(X-\mu)/(\sigma)=(695-500)/(100)=(195)/(100)=1.95\\\\\\P(X>695)=P(z>1.95)=0.026`

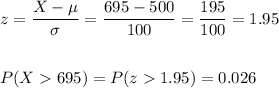
a. We want to calculate the probability that a randomly selected student scores at most 485.

We calculate the z-score and then we calculate the probability:

`z=(X-\mu)/(\sigma)=(485-500)/(100)=(-15)/(100)=-0.15\\\\\\P(X<485)=P(z<-0.15)=0.44`