Answer:
- Iron (III) oxide is the limiting reactant.
-
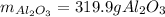
-
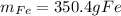
Step-by-step explanation:
Hello,
In this case, we consider the following reaction:
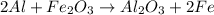
Thus, for identifying the limiting reactant we should compute the available moles of aluminium in 268 g:
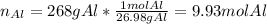
Next, we compute the moles of aluminium that are consumed by 501 grams of iron (III) oxide via their 2:1 molar ratio:
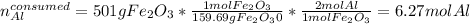
Thus, we notice there are less consumed moles of aluminium than available, for that reason, it is in excess; therefore, the iron (III) oxide is the limiting reactant.
Moreover, the theoretical mass of aluminium oxide is:
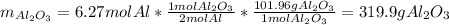
And the theoretical mass of iron is:
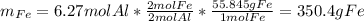
Best regards.