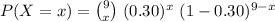Question

Suppose that for a randomly selected high school student who has taken a college entrance exam, the probability of scoring above 650 is 0.30. A random sample of n = 9 students was selected. The probability that at exactly ____ of the students scored over 650 points is found using:

Answer 1

7

Explanation:

Answer on learning curve

Answer 2

The formula to compute the probability that at exactly x of the students scored over 650 points is:

`P(X=x)={9\choose x}\ (0.30)^(x)\ (1-0.30)^(9-x)`

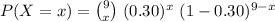
Explanation:

Let the random variable X represent the number of students who scored above 650 in the college entrance exam.

The probability that a student scored above 650 in the college entrance exam is, p = 0.30.

A random sample of n = 9 students was selected.

The events of any student scoring above 650 in the college entrance exam is independent of the others.

The random variable X follows a Binomial distribution with parameters n = 9 and p = 0.30.

The probability mass function of X is:

`P(X=x)={9\choose x}\ (0.30)^(x)\ (1-0.30)^(9-x);\ x=0,1,2,3...`

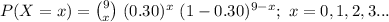
Thus, the formula to compute the probability that at exactly x of the students scored over 650 points is:

`P(X=x)={9\choose x}\ (0.30)^(x)\ (1-0.30)^(9-x)`