Question

6. To isolate benzoic acid from a bicarbonate solution, it is acidified with concen- trated hydrochloric acid, as in experiment 1. What volume of acid is needed to neutralize the bicarbonate

Answer 1

For our assumed experiment; the expected volume of Hcl acid needed to neutralize the bicarbonate is 0.13 mL

Step-by-step explanation:

We are going attempt this question experimentally.

We know that benzoic acid originate from the relationship between benzene and a carboxylic group. So basically , the functional group of a carboxylic acid (-COOH) joins with a benzene ring(C₆H₆) to form a simple aromatic carboxylic acid known as Benzoic acid. (C₇H₆O₂)

However, it is possible to isolate benzoic acid from a bicarbonate solution in the presence of an acidified concentrated hydrochloric acid.

Let assume that ;

0.20 g of benzoic acid was reacted with 2 mL of a 20% solution of NaHCO₃, the amount of the excess NaHCO₃ can be determined by subtracting the amount of benzoic acid from the amount of NaHCO₃.

Let first calculate the number of moles in 0.20 g of benzoic acid

we know that the standard molar mass of benzoic acid is 122.12 g/mol

number of moles of benzoic acid = mass of benzoic acid/molar mass of benzoic acid =

number of moles of benzoic acid = 0.20/ 122.12

number of moles of benzoic acid = 0.0016 mol

number of moles of bicarbonate solution = mass of bicarbonate solution/ molar mass of bicarbonate solution

number of moles of bicarbonate solution = 0.2/84.00654 g/mol

number of moles of bicarbonate solution = 0.00238 mol

∴

(0.00238 - 0.0016) mol

= 7.8 × 10⁻⁴ mol

Let assume that the concentrated HCl is 12 M

Also. HCl and NaHCO₃ react together at the ratio of 1:1; thus the volume of Hcl acid needed to neutralize the bicarbonate is:

`= ( 7.8 * 10^(-4) \ \ mol )* ( (2\ L)/( 12 \ M))*( (10^3 \mL)/(1 \ L))`

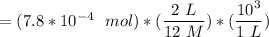
= 0.13 mL

Thus; for our assumed experiment; the expected volume of Hcl acid needed to neutralize the bicarbonate is 0.13 mL