Answer:
the magnitude of the stress necessary to cause slip to occur on the (111) plane in the
![[1 0 \overline 1]](https://img.qammunity.org/2021/formulas/engineering/college/czyhne3kqjbyzbrrzs047bqicuvz99v38t.png) direction is 4.85 MPa
direction is 4.85 MPa
Step-by-step explanation:
From the given information;
To determine the angle
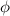 between the direction [100] and [111]; we have:
between the direction [100] and [111]; we have:
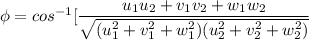
where;
[u₁,v₁,w₁] and [u₂, v₂, w₂] are directional indices.
replacing 1 for u₁ , 0 for v₁ and 0 for w₁ ;
also replacing 1 for u₂, 1 for v₂ and 1 for w₂ ; we have :
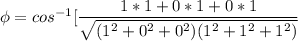
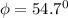
To determine the angle
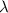 for the slip direction
for the slip direction
![[1 0 \overline 1]](https://img.qammunity.org/2021/formulas/engineering/college/czyhne3kqjbyzbrrzs047bqicuvz99v38t.png)
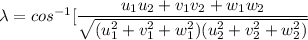
replacing 1 for u₁ , 0 for v₁ and 0 for w₁ ;
also replacing 1 for u₂, 1 for v₂ and -1 for w₂ ; we have :
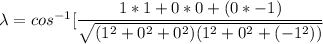
![\phi = cos ^(-1) [(1)/(√(2))]](https://img.qammunity.org/2021/formulas/engineering/college/gyienmeawlx4gkx6mystraw8m16n07n1th.png)
The yield strength for the slip process
![[1 0 \overline 1]](https://img.qammunity.org/2021/formulas/engineering/college/czyhne3kqjbyzbrrzs047bqicuvz99v38t.png) can now be calculated as:
can now be calculated as:
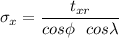
where
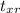 = 1.98 MPa
= 1.98 MPa
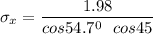
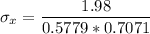
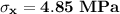
Hence, the magnitude of the stress necessary to cause slip to occur on the (111) plane in the
![[1 0 \overline 1]](https://img.qammunity.org/2021/formulas/engineering/college/czyhne3kqjbyzbrrzs047bqicuvz99v38t.png) direction is 4.85 MPa
direction is 4.85 MPa