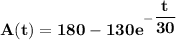Question

A tank contains 180 liters of fluid in which 50 grams of salt is dissolved. Brine containing 1 gram of salt per liter is then pumped into the tank at a rate of 6 L/min; the well-mixed solution is pumped out at the same rate. Find the number A(t) of grams of salt in the tank at time t.

Answer 1

`\mathbf{A(t) = 180 - 130e ^{-(t)/(30)}}`

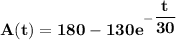
Explanation:

Given that:

A tank contains 180 liters of fluid in which 50 grams dissolved inside.

Brine containing 1 gram of salt per liter is then pumped into the tank at a rate of 6 L/min

The salt pumped out
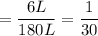`= (6 L)/(180 L) = (1)/(30)` of initial amount added salt

At (t = 0) = 50

To determine the number A (t)

`(dA)/(dt)=Rate_(in) - Rate _(out)`

`A' = 6 - (1)/(30)A`

`A' + (1)/(30)A = 6`

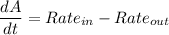
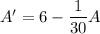
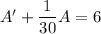
Integrating factor
`y = e^{\int\limits pdt`

`y = e^{\int\limits (1)/(30)dt}`

`y = e^{(t)/(30)}`

`(e^{ (t)/(30)}A)' =4 e ^{(t)/(30)}+c`

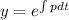
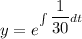
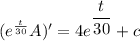
Taking integral on the both sides;

`Ae ^{(t)/(30)}= 6 * 30 e^{(t)/(30)} + c`

`A = 180+ ce^ {-(t)/(30)}`

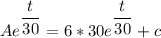
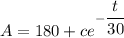
At A(t = 0) = 50

50 = 180 + C (assuming C =
`ce ^{-(t)/(30)}`)

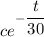C = 50 - 180

C = 130

`\mathbf{A(t) = 180 - 130e ^{-(t)/(30)}}`