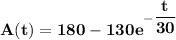Answer:
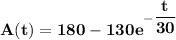
Explanation:
Given that:
A tank contains 180 liters of fluid in which 50 grams dissolved inside.
Brine containing 1 gram of salt per liter is then pumped into the tank at a rate of 6 L/min
The salt pumped out
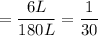 of initial amount added salt
of initial amount added salt
At (t = 0) = 50
To determine the number A (t)
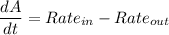
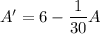
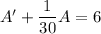
Integrating factor
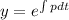
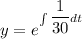
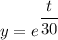
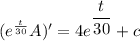
Taking integral on the both sides;
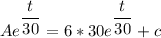
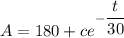
At A(t = 0) = 50
50 = 180 + C (assuming C =
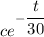 )
)
C = 50 - 180
C = 130