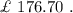Answer: The cost to buy all the paint he needs =
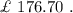
Explanation:
Formula: Area of trapezium =
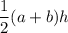 , where a and b are the parallel sides and h is the height.
, where a and b are the parallel sides and h is the height.
From the given figure of trapezium, we have
a = 10 m
b = 16 m
h = 7.6 m
Then, area of trapezium floor =
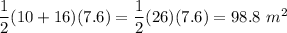
Also, 1 litre paint is required to paint and area of
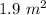 .
.
Then, the amount of paint required to paint
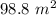 area =
area =
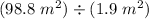
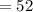 litres
litres
Since cost if 5 litres of paint =
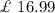
then cost of 1 liter paint =
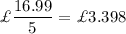
Then, cost of 52 litres of paint =
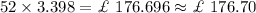
Hence, the cost to buy all the paint he needs =