Answer:
The area of the shaded region between
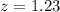 and
and
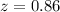 is
is
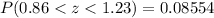 or 8.554%.
or 8.554%.
Step-by-step explanation:
To solve this question, we need to find the corresponding probabilities for the standardized values (or z-scores) z = 1.23 and z = 0.86, and then subtract both to obtain the area of the shaded region between these two z-scores.
We need to having into account that a z-score is given by the following formula:

Where
- x is a raw score from the distribution that we want to standardize using [1].
 is the mean of the normal distribution.
is the mean of the normal distribution.
 is the standard deviation of the normal distribution.
is the standard deviation of the normal distribution.
A z-score indicates the distance of x from the mean in standard deviations units, where a positive value "tell us" that x is above
 , and conversely, a negative that x is below
, and conversely, a negative that x is below
 .
.
The standard normal distribution is a normal distribution with
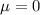 and
and
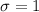 , and has probabilities for standardized values obtained using [1]. All these probabilities are tabulated in the standard normal table (available in any Statistical book or on the Internet).
, and has probabilities for standardized values obtained using [1]. All these probabilities are tabulated in the standard normal table (available in any Statistical book or on the Internet).
Using the cumulative standard normal table, for
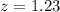 , the corresponding cumulative probability is:
, the corresponding cumulative probability is:
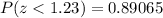
The steps are as follows:
- Consult the cumulative standard table using z = 1.2 as an entry. Z-scores are in the first column of the mentioned table.
- In the first row of it we have +0.00, +0.01, +0.02 and, finally, +0.03. The probability is the point that result from the intersection of z = 1.2 and +0.03 in the table, which is
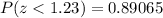 .
.
Following the same procedure, the cumulative probability for
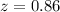 is:
is:
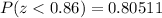
Subtracting both probabilities (because we need to know the area between these two values) we finally obtain the corresponding area between them (two z-scores):
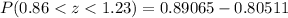
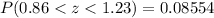
Therefore, the area of the shaded region between
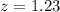 and
and
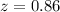 is
is
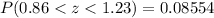 or 8.554%.
or 8.554%.
We can see this resulting area (red shaded area) in the graph below for a standard normal distribution,
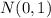 , and
, and
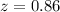 and
and
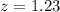 .
.