Question Correction
A circle is inscribed in a regular hexagon with side length 10 feet. What is the area of the shaded region? Recall that in a 30–60–90 triangle, if the shortest leg measures x units, then the longer leg measures
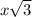 units and the hypotenuse measures 2x units.
units and the hypotenuse measures 2x units.
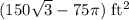
- (300 – 75π)
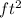
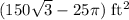
- (300 – 25π) ft2
Answer:
(A)
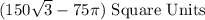
Explanation:
Area of the Shaded region =Area of Hexagon-Area of the Circle
Area of Hexagon
Length of the shorter Leg = x ft
Side Length of the Hexagon =10 feet
Perimeter of the Hexagon = 10*6 =60 feet
Apothem of the Hexagon (Length of the longer leg)
=
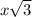 feet
feet
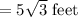
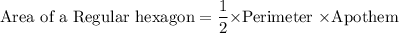
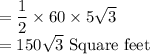
Area of Circle
The radius of the Circle = Apothem of the Hexagon
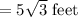
Area of the Circle
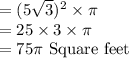
Therefore:
Area of the Shaded region