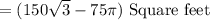Question

Ide length

Recall that in a 30° -60° - 90° triangle, if the shortest leg


measures x units, then the longer leg measures x/5 units


and the hypotenuse measures 2x units.


(150/3 – 757) ita


(300 - 757) ft


(150/3 - 257) ft


(300 - 257) ft?



Help out

Answer 1

it’s A

Explanation:

i took the test

Answer 2

Question Correction

A circle is inscribed in a regular hexagon with side length 10 feet. What is the area of the shaded region? Recall that in a 30–60–90 triangle, if the shortest leg measures x units, then the longer leg measures
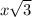`x√(3)` units and the hypotenuse measures 2x units.

• 
  `(150√(3)-75\pi) $ ft^2`
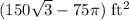
• (300 – 75π)
  `ft^2`
• 
  `(150√(3)-25\pi) $ ft^2`
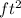
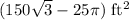
• (300 – 25π) ft2

Answer:

(A)
`(150√(3)-75\pi) $ Square Units`

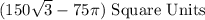
Explanation:

Area of the Shaded region =Area of Hexagon-Area of the Circle

Area of Hexagon

Length of the shorter Leg = x ft

Side Length of the Hexagon =10 feet

Perimeter of the Hexagon = 10*6 =60 feet

Apothem of the Hexagon (Length of the longer leg)

=
`x√(3)` feet

`=5√(3)$ feet`

`\text{Area of a Regular hexagon}=(1)/(2) * $Perimeter * $Apothem`

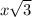`=(1)/(2) * 60 * 5√(3)\\=150√(3)$ Square feet`

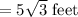
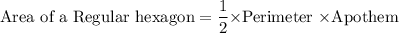
Area of Circle

The radius of the Circle = Apothem of the Hexagon
`=5√(3)$ feet`

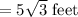
Area of the Circle

`=(5√(3))^2 * \pi\\ =25 * 3 * \pi\\=75\pi $ Square feet`

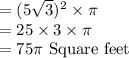
Therefore:

Area of the Shaded region
`= (150√(3)-75\pi) $ Square feet`