Question

If the 1550-lb boom AB, the 190-lb cage BCD, and the 169-lb man have centers of gravity located at points G1, G2 and G3, respectively, determine the resultant moment produced by all the weights about point A.

Answer 1

hello the required diagram is missing attached to the answer is the required diagram

7.9954 kip.ft

Step-by-step explanation:

AB = 1550-Ib ( weight acting on AB )

BCD = 190 - Ib ( weight of cage )

169-Ib = weight of man inside cage

Attached is the free hand diagram of the question

calculate distance
`x!`

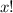
= cos 75⁰ =
`(x^!)/(10ft)`

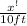
`x! = 10 * cos 75^(o)` = 2.59 ft

calculate distance x

= cos 75⁰ =
`(x)/(30ft)`

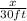
x = 30 * cos 75⁰ = 7.765 ft

The resultant moment produced by all the weights about point A

∑ Ma = 0

Ma = 1550 *
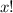`x!` + 190 ( x + 2.5 ) + 169 ( x + 2.5 + 1.75 )

Ma = 1550 * 2.59 + 190 ( 7.765 + 2.5 ) + 169 ( 7.765 + 2.5 + 1.75 )

= 4014.5 + 1950.35 + 2030.535

= 7995.385 ft. Ib ≈ 7.9954 kip.ft