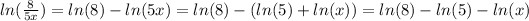Answer:
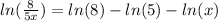
Explanation:
Use the properties of logarithms on each step:
First use the property for the logarithm of a quotient:
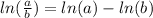
So we get:
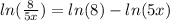
Now, we can expand the last term using the property of logarithm of a product:
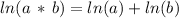
Therefore we write
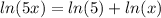
No we insert this result in the subtraction we had before: