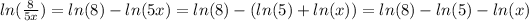Question

Expand the expression: ln 8/5x

Answer 1

`ln((8)/(5x) )=ln(8)-ln(5)-ln(x)`

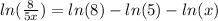
Explanation:

Use the properties of logarithms on each step:

First use the property for the logarithm of a quotient:

`ln((a)/(b) )=ln(a)-ln(b)`

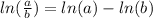
So we get:
`ln((8)/(5x) )=ln(8)-ln(5x)`

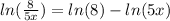
Now, we can expand the last term using the property of logarithm of a product:

`ln(a\,*\,b)=ln(a)+ln(b)`

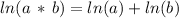
Therefore we write
`ln(5x)=ln(5)+ln(x)`

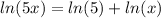
No we insert this result in the subtraction we had before:

`ln((8)/(5x) )=ln(8)-ln(5x)=ln(8)-(ln(5)+ln(x))=ln(8)-ln(5)-ln(x)`