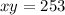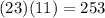Answer:
11 y 23
Explanation:
Nombrando los números como
 y
y
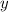 ,
,
Planteamos las siguientes ecuaciones:
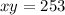 (el producto de los numeros es 253)
(el producto de los numeros es 253)
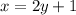 (uno de los enteros debe ser uno más que el doble del otro).
(uno de los enteros debe ser uno más que el doble del otro).
Sustituimos la segunda ecuación en la primera:
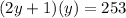
resolvemos para encontrar y:
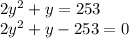
usando la formula general para resolver la ecuación cuadrática:
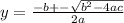
donde
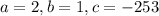
Sustituyendo los valores:
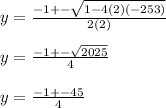
usando el signo mas obtenemos que y es:
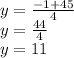
(no usamos el signo menos, debido a que obtendriamos fracciones y buscamos numeros enteros)
con este valor de y, podemos encontrar x usando:
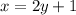
sustituimos
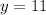
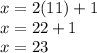
y comprobamos que el producto sea 253: