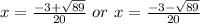Question

Which equation can be solved using the expression StartFraction negative 3 plus-or-minus StartRoot (3) squared + 4 (10) (2) EndRoot Over 2 (10) EndFraction for x?

Answer 1

B) 2 = 3x + 10
`x^(2)`

Explanation:

took the test

Answer 2

A quadratic equation

Explanation:

Given

`(-3 +- √(3^2 + 4(10)(2)))/(2(10))`

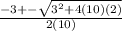
Required

Which equation can be solved using the above expression

Using the above expression, the equation that can be solved is the roots of a quadratic equation

The general format of the roots of a quadratic equation is given as

`x= (-b +- √(b^2- 4ac))/(2a)`

When
`x= (-b +- √(b^2- 4ac))/(2a)` is compared to
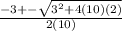`(-3 +- √(3^2 + 4(10)(2)))/(2(10))`, one would observe that they have the same format;

Solving
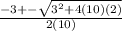`(-3 +- √(3^2 + 4(10)(2)))/(2(10))` further to get the values of x

`x = (-3 +- √(3^2 + 4(10)(2)))/(2(10))`

`x = (-3 +- √(9 + 4*10*2))/(2*10)`

`x = (-3 +- √(9 + 80))/(20)`

`x = (-3 +- √(89))/(20)`

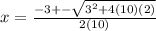
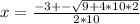
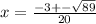
So;

`x = (-3 + √(89))/(20) \ or \ x = (-3 - √(89))/(20)`