Question

We have a bag containing 4 yellow, 5 green and 6 orange candies. We draw two candies without replacement.

Find the probability of getting both candies green

Answer 1

9.52% probability of getting both candies green

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the candies are selected is not important. They are also selected without replacement. So we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Find the probability of getting both candies green

Desired outcomes:

2 green, from a set of 5. So

`D = C_(5,2) = (5!)/(2!3!) = 10`

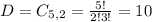
Total outcomes:

2 from a set of 4+5+6 = 15. So

`T = C_(15,2) = (15!)/(2!13!) = 105`

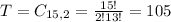
Probability:

`p = (D)/(T) = (10)/(105) = 0.0952`

9.52% probability of getting both candies green