Answer:
Step-by-step explanation:
Given that:
Torque T = 2300 lb - ft
Bending moment M = 1500 lb - ft
axial thrust P = 2500 lb
yield points for tension σY= 100 ksi
yield points for shear τY = 50 ksi
Using maximum-shear-stress theory

where;
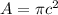
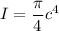
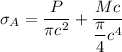
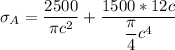
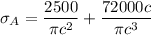
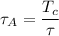
where;
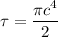
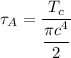

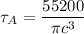
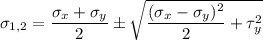
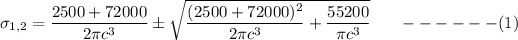
Let say :

Then :
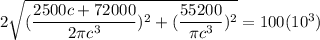
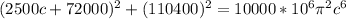
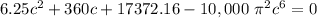
According to trial and error;
c = 0.75057 in
Replacing c into equation (1)


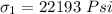
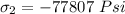
The required diameter d = 2c
d = 1.50 in or 0.125 ft