Answer:
55.3
Step-by-step explanation:
The computation of the number of bright-dark-bright fringe shifts observed is shown below:
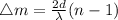
where
d =
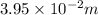
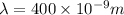
n = 1.00028
Now placing these values to the above formula
So, the number of bright-dark-bright fringe shifts observed is
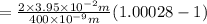
= 55.3
We simply applied the above formula so that the number of bright dark bright fringe shifts could come