Answer:
The calculated value Z = 1.2903 < 1.96 at 0.05 level of significance
Null hypothesis is accepted at 0.05 level of significance
The population proportion is equal to 0.5
Explanation:
Step (i):-
Given random sample size ' n' = 250
Sample proportion 'p'

Given Population proportion P = 0.5
Q = 1-P = 1-0.5 =0.5
Null Hypothesis : H₀ : P = 0.5
Alternative Hypothesis : H₁ : P≥ 0.5
Step(ii):-
Test statistic

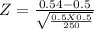
Z = 1.2903
Level of significance α = 0.05
Z₀.₀₅ = 1.96
The calculated value Z = 1.2903 < 1.96 at 0.05 level of significance
Null hypothesis is accepted at 0.05 level of significance
Step(iii):-
P- value
The probability of test statistic
P(Z > 1.2903) = 0.5 - A ( 1.2903)
= 0.5 - 0.4015
= 0.0985≅ 0.10
i) P- value =0.10 > α = 0.05
null hypothesis is accepted
Conclusion:-
The population proportion is equal to 0.5