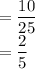Answer:
(a)10 Outcomes
(b)

Explanation:
An urn contains two blue balls (denoted
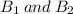 ) and three white balls (denoted
) and three white balls (denoted
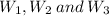 ).
).
In the selection, a ball is picked and replaced.
The possible outcomes of the experiment are:
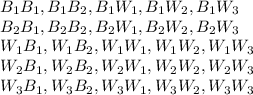
(a)If the first ball drawn is blue. the outcomes are:
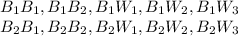
There are 10 outcomes if the first ball drawn is blue.
Probability that the first ball drawn is blue