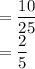Question

An urn contains two blue balls (denoted B1 and B2) and three white balls (denoted W1, W2, and W3). One ball is drawn from the urn, its color recorded, and is replaced. Another ball is then drawn and its color recorded. Let B1W2 denote the outcome that the first ball drawn is B1 and the second ball drawn is W2. Because the first ball is replaced before the second ball is drawn, the outcomes of the experiment are equally likely. List all 25 possible outcomes of the experiment on a sheet of paper. (a) Consider the event that the first ball that is drawn is blue. Count all the outcomes in this event.

Answer 1

(a)10 Outcomes

(b)
`(2)/(5)`

Explanation:

An urn contains two blue balls (denoted
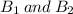`B_1 \:and\: B_2`) and three white balls (denoted
`W_1, W_2 \:and\: W_3`).

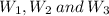In the selection, a ball is picked and replaced.

The possible outcomes of the experiment are:

`B_1B_1,B_1B_2,B_1W_1,B_1W_2,B_1W_3\\B_2B_1,B_2B_2,B_2W_1,B_2W_2,B_2W_3\\W_1B_1,W_1B_2,W_1W_1,W_1W_2,W_1W_3\\W_2B_1,W_2B_2,W_2W_1,W_2W_2,W_2W_3\\W_3B_1,W_3B_2,W_3W_1,W_3W_2,W_3W_3`

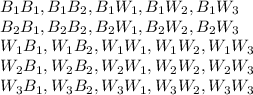
(a)If the first ball drawn is blue. the outcomes are:

`B_1B_1,B_1B_2,B_1W_1,B_1W_2,B_1W_3\\B_2B_1,B_2B_2,B_2W_1,B_2W_2,B_2W_3`

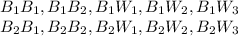
There are 10 outcomes if the first ball drawn is blue.

Probability that the first ball drawn is blue

`=(10)/(25)\\ =(2)/(5)`