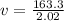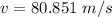Answer:
a The speed of the plane is
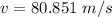
b The altitude of the plane is
Step-by-step explanation:
Let the altitude of the plane is Z
The distance at which the plane hears the horn is
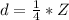
The time taken for the sound to reach the plane is
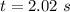
The speed of sound is
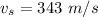
The distance from the point the plane hears the sound to the boat is mathematically evaluated as
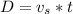
substituting values

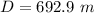
This is the diagonal distance of the boat to the plane (hypotenuse)
The altitude of the plane is the vertical distance of the plane from the boat
and the horizontal distance of the plane from the boat is d
Applying Pythagoras theorem
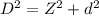
=>
![D^2 = Z^2 +[ (1)/(4) * Z ]^2](https://img.qammunity.org/2021/formulas/physics/college/re0szjn673f3y2hmtcmcqgswd09r4o9h0a.png)
substituting values

=>
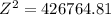
=>
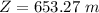
=>
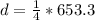
=>
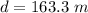
Now the velocity of the plane is