Question

Use variation of parameters to find a general solution to the differential equation given that the functions y1 and y2 are linearly independent solutions to the corresponding homogeneous equation for t > 0. ty" + (2t - 1 )y' - 2y = 6t^2 e^-2t​; y1 = 22t −​1, y2 = e^-2t

Answer 1

`y_g(t) = c_1*( 2t - 1 ) + c_2*e^(^-^2^t^) - e^(^-^2^t^)* [ t^3 + (3)/(4)t^2 + (3)/(4)t ]`

Explanation:

Solution:-

- Given is the 2nd order linear ODE as follows:

`ty'' + ( 2t - 1 )*y' - 2y = 6t^2 . e^(^-^2^t^)`

- The complementary two independent solution to the homogeneous 2nd order linear ODE are given as follows:

`y_1(t) = 2t - 1\\\\y_2 (t ) = e^-^2^t`

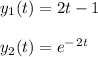
- The particular solution ( yp ) to the non-homogeneous 2nd order linear ODE is expressed as:

`y_p(t) = u_1(t)*y_1(t) + u_2(t)*y_2(t)`

Where,

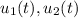`u_1(t) , u_2(t)` are linearly independent functions of parameter ( t )

- To determine [
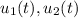`u_1(t) , u_2(t)` ], we will employ the use of wronskian ( W ).

- The functions [
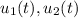`u_1(t) , u_2(t)` ] are defined as:

`u_1(t) = - \int {(F(t). y_2(t))/(W [ y_1(t) , y_2(t) ]) } \, dt \\\\u_2(t) = \int {(F(t). y_1(t))/(W [ y_1(t) , y_2(t) ]) } \, dt \\`

Where,

F(t): Non-homogeneous part of the ODE

W [ y1(t) , y2(t) ]: the wronskian of independent complementary solutions

- To compute the wronskian W [ y1(t) , y2(t) ] we will follow the procedure to find the determinant of the matrix below:

`W [ y_1 ( t ) , y_2(t) ] = | \left[\begin{array}{cc}y_1(t)&y_2(t)\\y'_1(t)&y'_2(t)\end{array}\right] |`

`W [ (2t-1) , (e^-^2^t) ] = | \left[\begin{array}{cc}2t - 1&e^-^2^t\\2&-2e^-^2^t\end{array}\right] |\\\\W [ (2t-1) , (e^-^2^t) ]= [ (2t - 1 ) * (-2e^-^2^t) - ( e^-^2^t ) * (2 ) ]\\\\W [ (2t-1) , (e^-^2^t) ] = [ -4t*e^-^2^t ]\\`

- Now we will evaluate function. Using the relation given for u1(t) we have:

`u_1 (t ) = - \int {(6t^2*e^(^-^2^t^) . ( e^-^2^t))/(-4t*e^(^-^2^t^)) } \, dt\\\\u_1 (t ) = (3)/(2) \int [ t*e^(^-^2^t^) ] \, dt\\\\u_1 (t ) = (3)/(2)* [ ( -(1)/(2) t*e^(^-^2^t^) - \int {( -(1)/(2)*e^(^-^2^t^) )} \, dt] \\\\u_1 (t ) = -e^(^-^2^t^)* [ ( (3)/(4) t + (3)/(8) )] \\\\`

- Similarly for the function u2(t):

`u_2 (t ) = \int {(6t^2*e^(^-^2^t^) . ( 2t-1))/(-4t*e^(^-^2^t^)) } \, dt\\\\u_2 (t ) = -(3)/(2) \int [2t^2 -t ] \, dt\\\\u_2 (t ) = -(3)/(2)* [(2)/(3)t^3 - (1)/(2)t^2 ] \\\\u_2 (t ) = t^2 [(3)/(4) - t ]`

- We can now express the particular solution ( yp ) in the form expressed initially:

`y_p(t) = -e^(^-^2^t^)* [(3)/(2)t^2 + (3)/(4)t - (3)/(8) ] + e^(^-^2^t^)*[(3)/(4)t^2 - t^3 ]\\\\y_p(t) = -e^(^-^2^t^)* [t^3 + (3)/(4)t^2 + (3)/(4)t - (3)/(8) ] \\`

Where the term: 3/8 e^(-2t) is common to both complementary and particular solution; hence, dependent term is excluded from general solution.

- The general solution is the superposition of complementary and particular solution as follows:

`y_g(t) = y_c(t) + y_p(t)\\\\y_g(t) = c_1*( 2t - 1 ) + c_2*e^(^-^2^t^) - e^(^-^2^t^)* [ t^3 + (3)/(4)t^2 + (3)/(4)t ]`