Question

Sometimes a change of variable can be used to convert a differential equation y′=f(t,y) into a separable equation. One common change of variable technique is as follows. Consider a differential equation of the form y′=f(αt+βy+γ), where α,β, and γ are constants. Use the change of variable z=αt+βy+γ to rewrite the differential equation as a separable equation of the form z′=g(z). Solve the initial value problem

Answer 1

`y = - [ (1)/(t - (28)/(9) ) + t ]`

Explanation:

Solution:-

- A change of variable is a technique employed in solving many differential equations that are of the form: y ' = f ( t , y ).

- Considering a differential equation of the form y' = f ( αt + βy + γ ), where α, β, and γ are constants. A substitution of an arbitrary variable z = αt + βy + γ is made and the given differential equation is converted into a form: z ' = g ( z ).

- This substitution basically allow us to solve in-separable differential equations by converting them into a form that can be separated, followed by the set procedure.

- We are to solve the initial value problem for the following differential equation:

`y' = ( t + y ) ^2 - 1 , y ( 3 ) = 6`

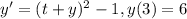
First Step: Make the appropriate substitution

- We will use a arbitrary variable ( z ) and define the our substitution by finding a multi-variable function f ( t , y ) that is a part of the given ODE.

- We see that the term ( t + y ) is a multi-variable function and also the culprit that doesn't allow us to separate our variables.

- Usually, the change of variable substitution is made for such " culprits ".

- So our substitution would be:

`z = t + y`

Second Step: Implicit differential of the substitution variable ( z ) with respect to the independent variable

- In the given ODE we see that the variable ( t ) is our independent variable. So we will derivate the supposed substitution as follows:

`(dz)/(dt) = 1 + (dy)/(dt) \\\\(dy)/(dt) = -1 + (dz)/(dt)`

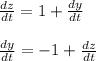
Remember: z is a multivariable function of "t" and "y". So we perform implicit differential for the variable " z ".

Third Step: Plug in the differential form in step 2 and change of variable substitution of ( z ) in the given ODE.

- The given ODE can be expressed as:

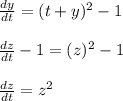`(dy)/(dt) = ( t + y ) ^2 - 1\\\\(dz)/(dt) - 1 = ( z ) ^2 - 1\\\\(dz)/(dt) = z ^2 \\` ... Separable ODE

Fourth Step: Separate the variables and solve the ODE.

- We see that the substitution left us with a simple separable ODE.

Note: If we do not arrive at a separable ODE, then we must go back and re-choose our change of variable substitution for ( z ).

- We will progress by solving our ODE:

`(dz)/(z^2) = dt\\\\\int {(1)/(z^2) } \, dz = \int {1} \, dt\\\\-(1)/(z) = t + c\\\\(1)/(z) = - (t + c )\\\\z = -(1)/(t + c)`

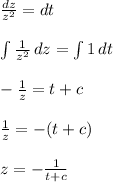
Where,

c: The constant of integration

Fifth Step: Back-substitution of variable ( z )

- We will now back-substitute the substitution made in the first step and arrive back at our original variables ( y and t ) as follows:

`t + y = - (1)/(t + c) \\\\y = - [ (1)/(t + c) + t ]`

Sixth Step: Apply the initial value problem and solve for the constant of integration ( c )

- We will use the given initial value statement i.e y ( 3 ) = 6 and evaluate the constant of integration ( c ) as follows:

`y ( 3 ) = - [ (1)/(3 + c) + 3 ] = 6 \\\\(1)/(3 + c) = -9\\\\3 + c = -(1)/(9) \\\\c = - (28)/(9)`

Seventh Step: Express the solution of the ODE in an explicit form ( if possible ):

`y = - [ (1)/(t - (28)/(9) ) + t ]`