Answer:
Correct answers:
A. An angle that measures
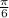 radians also measures
radians also measures
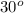
C. An angle that measures
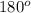 also measures
also measures
 radians
radians
Explanation:
Recall the formula to transform radians to degrees and vice-versa:
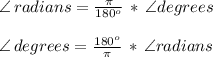
Therefore we can investigate each of the statements, and find that when we have a
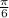 radians angle, then its degree formula becomes:
radians angle, then its degree formula becomes:
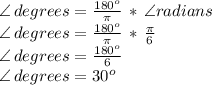
also when an angle measures
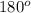 , its radian measure is:
, its radian measure is:
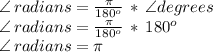
The other relationships are not true as per the conversion formulas