Answer:
They'll reach the same population in approximately 113.24 years.
Explanation:
Since both population grows at an exponential rate, then their population over the years can be found as:
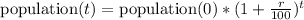
For the city of Anvil:
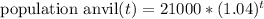
For the city of Brinker:
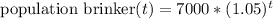
We need to find the value of "t" that satisfies:
![\text{population brinker}(t) = \text{population anvil}(t)\\21000*(1.04)^t = 7000*(1.05)^t\\ln[21000*(1.04)^t] = ln[7000*(1.05)^t]\\ln(21000) + t*ln(1.04) = ln(7000) + t*ln(1.05)\\9.952 + t*0.039 = 8.8536 + t*0.0487\\t*0.0487 - t*0.039 = 9.952 - 8.8536\\t*0.0097 = 1.0984\\t = (1.0984)/(0.0097)\\t = 113.24](https://img.qammunity.org/2021/formulas/mathematics/college/gj1dypepq5r3h556r0g1satdb50zynvnwl.png)
They'll reach the same population in approximately 113.24 years.