Answer:
Explanation:
The given function is

Zeroes of the function are
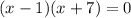
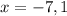
It means, f(x) intersect x-axis at x=-7 and x=1.
Mid value of -7 and 1 is the x-coordinate of the vertex.
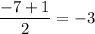
At x=-3,
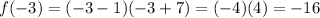
So, the vertex of the function is at (-3,-16).
The given function can be written as
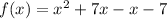
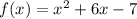
Here leading coefficient is negative, it means it is an upward parabola.
So, we conclude that
1. The graph is increasing on the interval x > -3.
2. The graph is decreasing on the interval x < -3.
3. The graph is positive only on the intervals where x <-7 and where x > 1.
4. The graph is negative only on the intervals where -7 < x < 1.
Therefore, the correct options are 2, 3 and 4.