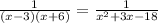Answer:
Four steps of multiplying the rational expressions and their examples are given below
Step 1
Factor the expression acting as the numerator and denominator of both functions
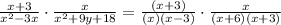
Step 2
Write both of the expression being multiplied as one expression

Step 3
Simplify the rational expression by cutting out the common terms
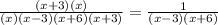
Step 4
Multiply any remaining factors in numerator or denominator.