Question

A 45 gram sample of a substance that's used to preserve fruit and vegetables has a k-value of 0.1088

Answer 1

6.4

Explanation:

I did it on the same site and got it correct

Answer 2

The substance's half-life is 6.4 days

Explanation:

Recall that the half life of a substance is given by the time it takes for the substance to reduce to half of its initial amount. So in this case, where they give you the constant k (0.1088) in the exponential form:

`N=N_0\,e^(-k\,*\,t)`

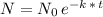
we can replace k by its value, and solve for the time "t" needed for the initial amount
`N_0` to reduce to half of its value (
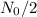`N_0/2`). Since the unknown resides in the exponent, to solve the equation we need to apply the natural logarithm:

`N=N_0\,e^(-k\,*\,t)\\(N_0)/(2) =N_0\,e^(-0.1088\,*\,t)\\(N_0)/(2\,*N_0) =e^(-0.1088\,*\,t)\\(1)/(2) =e^(-0.1088\,*\,t)\\ln((1)/(2) )=-0.1088\,t\\t=(ln((1)/(2) ))/(-0.1088) \\t=6.37\,\,days`

which rounded to the nearest tenth is: 6.4 days